Amazing Challenge I
By Shawn Olson
Posted on 12.18.03
As a kid I
used to draw mazes all the
time. Sometimes I would draw a couple dozen mazes and tape them
together, so that the entire maze was twenty feet long laid out. I
hadn't made any mazes in a long time, so I decided it's time to get
back in the habit. Here is the first maze in my series of Amazing
Challenges. Enjoy.
Click the image to view the maze full-size.
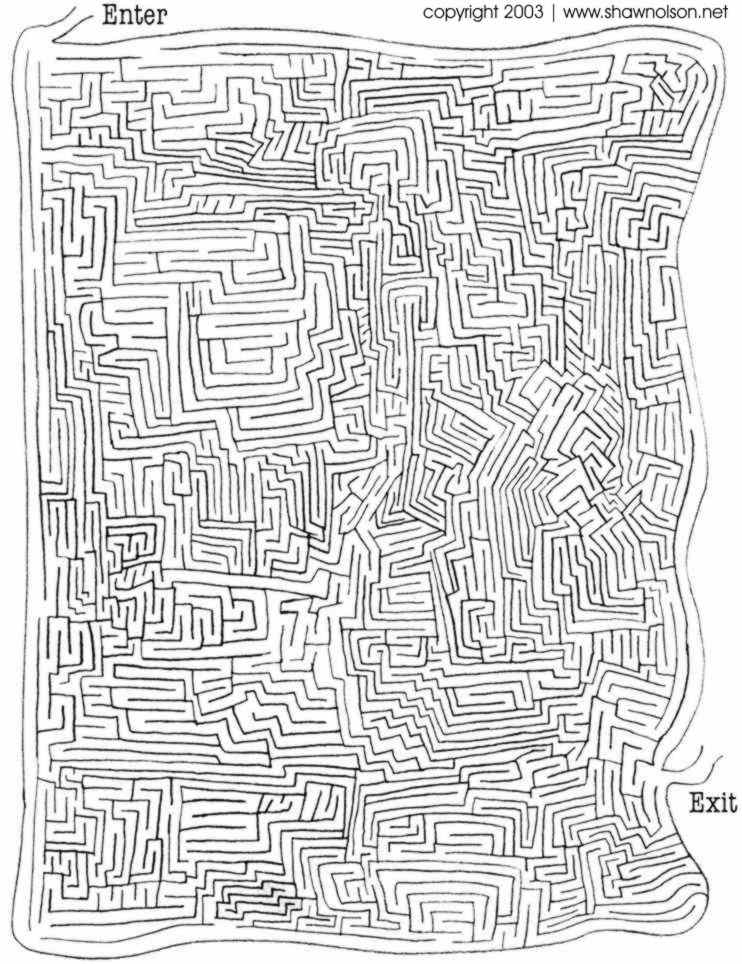
Copyright © 2003-2009 by Shawn
Olson.
*****************
Help the
Monarch butterfly fly south for the winter.
Back
to Fall mazes.
Be sure
to visit our
main printables index for more fun
including our Fall
coloring pages, word
puzzles and check out our great Fall
crafts!
Click here for printable version
More
fun printables and activities to enjoy:
****************************



 I also enjoy
creating mazes. Recently I've been focusing on creating
mazes on the surfaces of various geometric shapes (or, more accurately,
I've been focusing on creating computer programs which generate random
mazes of the surfaces of geometric shapes). Pictured to the right is a
maze on the surface of a "buckyball" (i.e. a truncated icosahedron, or
soccer ball).
I also enjoy
creating mazes. Recently I've been focusing on creating
mazes on the surfaces of various geometric shapes (or, more accurately,
I've been focusing on creating computer programs which generate random
mazes of the surfaces of geometric shapes). Pictured to the right is a
maze on the surface of a "buckyball" (i.e. a truncated icosahedron, or
soccer ball).
The maze
is "perfectly formed", meaning that there are no loops, and every spot
on the maze is reachable from every other spot on the maze. This is
really just a prototype; I plan to make a nicer one with a solid wood
structure beneath the laminated paper surface. The pictured one is
simply heavy paper laminated with clear contact paper and taped at the
edges of tha faces. The laminate allows one to use an erasable marker
on the surface when solving.
I created
a maze on the surface
of a cube for my first Puzzle
Party back in fall of 2004. I did not have one at EPP2, but I
expect similar puzzles to crop up again at future Parties.
***********





www.TeamOfMonkeys.com
Your
source for mazes.
Hallucamazenic - Ink On Paper,
Winter 2006, by Y. Frimer

Click
here to buy Maze A Delic Royalty Free License - For Editorial and
Commericial Use








TeamOfMonkeys.com
***********************
Adapted
from Business Mazes by Joni Farthing, Hart-Davis, 1981

What is
a maze?
A maze is
a puzzling game. A garden maze is a network, or labyrinth, of paths
between high hedges. The puzzle is to find the paths that will lead
most quickly to the exit, but the hedges prevent you from seeing where
alternative routes lead.
How to
read a maze
There are
five mazes designed to introduce and practise language common in
business situations. Just like the garden maze, each one involves
making decisions. However, the aim is not to reach the exit as quickly
as possible, but to solve the problem effectively.
The
entrance is 'the situation'. Everyone starts here, and then chooses a
course of action from 1. If none of the alternatives are exactly the
path you would like to take, choose the one nearest to the ideal. Each
decision leads to another number in the maze, which shows how the
situation has changed because of the action you have taken. Write down
every number you turn to. This is your numbers-route, (If you find
yourself on a familiar path, think again!) Continue until the end, or
exit, of the maze is reached.
In a
garden maze you cannot use a ladder to take a quick look over the hedge
to see where other paths lead. In this book, you should not look at
routes unless they are indicated by your decisions.
I suggest
that you work through the maze in a group, but you can do it by
yourself, discussing each choice in detail before reaching a joint
decision and going to the next stage. Practise your English by trying
to convince others that your point of view is right, but listen to
their opinions too. Keep a record of the problems and your decisions.
After you finish the maze you can either discuss it further or go back
along your number-route and take another look at the unfamiliar words
and expressions you met on your way. Write a report when you have
finished.
No
Smoking
The
Salesman
The
Complaint
The
Reference
Reg
Collins
Random Maze
Here is a
random maze I have generated by Monte Carlo. Can you find the way
out?

In reality,
a random maze would be much more convoluted than the above
example.
Such mazes are less pleasing to the eye. In the case above a maze
consisting of walls that spiral from the origin was generated, and then
subjected to a Monte Carlo simulation for a short time (before the maze
would randomize completely).
Random
Tree:
A maze is a
special kind of random tree: in particular, it is a spanning tree
of a
square in the square lattice (such a maze would have only one way out
from the center). Below is a random tree in the square lattice.

Towards
the limiting random lattice tree
If the
number of edges in the tree above should be multiplied, while the
length scale is shrunk appropriately, a limiting random tree will be
seen. In the picture below there are 10000 edges, each too small
to be
seen here, in a lattice tree generated by a Monte Carlo program.
The
tree begins to appear like a fractal object. The existence of a
scaling limit is known in high dimensions (above 8). There is
general
consensus that it also exists in dimensions below 9.

Random
Disks
The
interior of a closed loop in the square lattice (or a polygon) is a
Disk. In this example, a square lattice polygon was randomized by
subjecting it to a Metropolis Monte Carlo algorithm. The interior
of
the polygon is a disk.
Die
Oranje Vrystaat.
Die foto is
in die Noord Vrystaat geneem.

************************
Part 3 -
Tile-Based Graphics, and Maze Creation
Often
in game creation it becomes necessary to create multiple sets of game
graphics and background images which contain similar details and
repeating elements. It may be for a HUGE outdoor overhead map for a
role-playing game showing landmarks, hills, trees, grass, monsters,
etc., or as in our case, a bunch of similarly-constructed mazes, or
whatever. As game designers and programmers, we need to be able to
store, manipulate, and recreate these in our game, using as few
graphic, memory, and hard disk storage resources as possible.
One
common way of doing this is called "Tokenizing" the image. Instead of
saving and loading all the images we could possibly need for our game,
we break the image down into a small number of replicable parts - a set
of graphic pieces that we can arrange to create the image we need when
we need it. Usually, most pieces in this set are the same size, and
will match up against other pieces in the set. The graphic pieces are
generally called "tiles." The graphic screens are stored as a matrix of
alphanumeric characters, called "tokens," with each character in the
matrix corresponding to one of the graphic tiles.
Here are the mazes I
have created so far for Snack Attack!

The
first "maze" is for the About this Game screen. The ghosts chase Snacky
around the About this Game text. The next maze (top, middle) is the
original Pacman maze, resized to fit our game window. The next four
mazes (the red, purple, green, and brown ones) are the original mazes
from Ms.Pacman, and the last two I found in hacked MsPacman roms on the
net.
Looking
at the mazes, you'll see that they all contain similar elements -
rounded ends, right angle bends, segments that are the same length,
etc.. To create these mazes, I took screen shots of the Pacman, et al,
mazes and cut them up into 24 chunks. These 24 pieces arranged
carefully, can recreate any maze a Pacman game can run.
Once
I knew what the pieces needed to look like, I had to determine how to
create a set we can use for our game. I had to make some creative and
technical decisions to make the game easier to do and to make the mazes
"fit" in our game window.

The
mazes in the Pacman Arcade game are 1.5 times as tall as they are wide,
and our game window is roughly square in mode 19, which has a 3:4
aspect ratio. In the Original, the maze borders are thinner than the
maze obstacles, and the vertical spacing between obstacles alternates
between high and short as we go from top to bottom in the maze. To
limit the number of tiles we'd need and to make maze creation and AI
programming easier, I decided to have one set of tiles for everything,
and to make all the tiles the same size. Notice our borders and
obstacles are the same thickness.
After
a couple hours of tweaking, I determined the "correct" matrix size for
our game is 19x22, with tiles that are 12x8 pixels in size. My primary
criteria was being able to reproduce the original Pacman maze using
uniform-sized tiles, and this maze needed to fit in a square game
window as close as possible to the screen size we have. Our game window
is about 8 pixels shorter than my other games, so I added the light
blue border box around the game window, centered it, and adjusted the
size of our feedback window to make it balance better. Since our Maze
tiles are 12x8, for consistency sake, I set the graphics size for all
the moving sprites to also be 12x8. This really is arbitrary, but it
makes keeping track of them easier. Another upshot of having 12x8 tiles
is we end up with about 1/3 fewer dots than the original.
Here is our minimum
tile set:
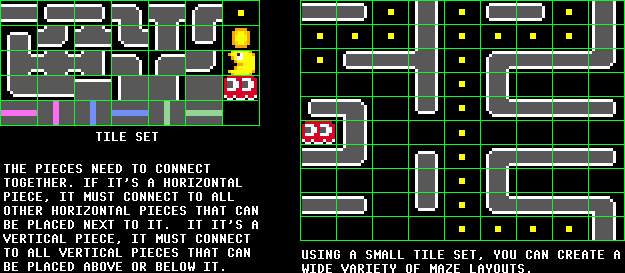
Notice
that our tile set is not colored. In the game we need to draw the mazes
in different colors, so our tile set here is black, white, and gray.
When we draw the maze we'll color the white and gray pixels in each
tile to the outline and interior color, respectively. Here I'm showing
you the 2D "arcade" tile set, because it's easier to see how it fits
together. I have a more solid, 3D pipes-look tile set in 10 colors that
will be included in the final version of the game. It was constructed
the same way, only I processed each tile in photoshop to make it look
3D like. We'll have a game option to choose between the two tile sets.
Our
tile set contains a few extra tiles to correspond with new features
we've added to the game. The 6 images along the bottom row are doors.
The first two are doors for the penalty box. In Pacman and MsPacman,
the penalty box is always in the same place, in the same orientation.
The reason I think is that they needed to hardcode the location so that
the ghost's eyes can find their way back to the box so that the ghosts
can respawn when we kill them. For our game, we can just have the eyes
target the Penalty box door, and they'll always find it, so we can put
the Penalty box anywhere in the maze and it can have a vertical
orientation if we want it to. Therefore I included a Horizontal and
Vertical Penalty box door.
The
next two doors are Ghost-Only doors. Snacky can't go through them. We
may want to make passages for the ghosts so they can ambush Snacky. The
last two doors are Snacky-only doors. We may want to block the ghosts
from certain Snacky-safe escape routes.
Included
in the tile set is a Dot, so we can place the dots only where we want
them. Similarly, we can place energizers anywhere we want, and since
Euphoria is flexible in redimentioning sequences, we can have as many
of them in the maze as we'd like.
Our
game will determine the starting positions and number of ghosts from
the maze definitions, so we can place as many ghosts as we want to,
anywhere in the maze. We MUST have a penalty box, with a Penalty Box
Door, but we can have the ghosts start from anywhere.
Snacky's starting
position will also be determined by the maze definition. We can start
the game with Snacky anywhere we want.
Tokenizing the
maze
Ok,
so we have a tile set that we can use to construct any maze we can
think of. So, how do we do it? I told you before that we want to
represent the maze as a matrix of alphanumeric characters with each
character corresponding to a tile in the tile set. Our mazes are 19x22
tiles big, and thus they can be represented by a matrix containing only
418 characters. That's pretty tight. Storing the mazes as a GIF image
is 6 times as large and GIFs are compressed pretty tightly.
How
do we choose the tokens for each tile? Arbitrarily. You can make any
alphanumeric character represent any tile you want. I usually try to go
for characters that look kinda like the tile, so when I look at the
text representation, I can tell what the maze is. Here is a maze from
Snack Attack! And it's corresponding text representation:
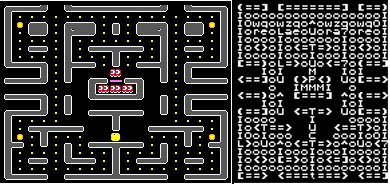
( is an upper left
corner,
) is an upper right
corner,
[ is a lower left
corner,
] is a lower right
corner,
< is a left ending
horizontal piece,
> is a right ending
horizontal piece.
O is an energizer and
o is a dot.
C is the player's
starting position - because C kinda looks like Snacky.
M is a Ghost (M for
Monster)
P is the Penalty Box
door.
= is a horizontal
piece.
You
get the idea. When I run out of characters that look like tiles, I just
start picking letters and symbols until I run out of tiles.
I
store all the levels in the game (in the maze order shown above) back
to back in one long sequence of sequences of sequences. Levels is all
of the mazes, Levels[1] is the about maze, Levels[3][4][5] is the token
at position 5,4 in the second level.(the red one in the image above -
third maze in the sequence)
For our purposes, I
have created a handy, dandy
maze editor
we can use to create the mazes. You click on the tile you want and then
place it in the game window. The program indexes into the maze
definition sequence and places the right token in the right place
automagically.
If you haven't yet
downloaded my version of
our course project, Snack Attack!, do
it now, and play it a million times to get an idea for the game.
*****************************

They are, of course, fun for all the family, although perhaps the
best thing about mazes is that they are often found in the grounds of
castles and stately homes so, while the adults explore the big house
and have a sneaky cream tea, the kids can get lost, literally.
However, the people who enjoy mazes the most – once they’ve been
persuaded into them – are the adults, who leave behind a life full of
decision-making only to be completely flummoxed by whether to turn left
or right.
One of the most famous mazes is at Hampton Court Palace in Surrey.
It attracts hundreds of thousands of visitors every year and is made of
hedges planted for William of Orange’s garden. You can read a fictional
account of it in Jerome K Jerome’s Three men in a boat. Another large
maze in beautiful surroundings is the yew maze at Chatsworth House near
Bakewell in Derbyshire.
York maze, the size of 15 football pitches, is thought to be the
largest in the world and has paths made out of 1.5million maize plants.
Special events include navigating the maze by torchlight, but like most
mazes, it is not open all year round so it is worth checking before you
go.
The best contemporary maze maker is Adrian Fisher, an Englishman who
helps farmers create mazes on their land and who designed the mazes at
Leeds Castle in Kent, Blenheim Palace in Oxfordshire and Scone Palace
in Perthshire.
There are more than 30 of his mazes around the country but one of
the best is Poplars Adventure Mega Maze in Knaresborough, North
Yorkshire.
Many of his mazes are great for families as they provide clues to
help you work out the route and each person is given a tall flag to
carry so they don’t lose each other – unless they want to, that it is.
For more information on the maze at Hampton Court Palace see www.hrp.org.uk
HamptonCourtPalace. Further details about York Maze can be found at www.yorkmaze.com.
For information about Poplars Adventure Mega Maze see www.poplarsmaze.co.uk.
**********************

Mazes in general (and hence algorithms to create Mazes)
can be organized along seven different classifications. These are:
Dimension, Hyperdimension, Topology, Tessellation, Routing, Texture,
and Focus.
A Maze can take one item from each of the classes in any combination.
Dimension: The dimension class is basically how many
dimensions
in space the Maze covers. Types are:
- 2D:
Most Mazes,
either on paper or life size, are this dimension, where it's always
possible to display the plan on the sheet of paper and navigate
it without overlapping any other passages in the Maze.
- 3D:
A three dimensional
Maze is one with multiple levels, where (in the orthogonal case
at least) passages may go up and down in addition to the four
compass directions. A 3D Maze is often displayed as an array of
2D levels, with "up" and "down" staircase
indicators.
- Higher
dimensions:
It's possible to have 4D and higher dimension Mazes. These are
often rendered as 3D Mazes, with special "portals" to
travel through the 4th dimension, e.g. "past" and "future"
portals.
- Weave:
A weave
Maze is basically a 2D (or more accurately a 2.5D) Maze, but where
passages can overlap each other. In display it's generally obvious
what's a dead end and what's a passage that goes under another.
Life size Mazes that have bridges connecting one portion of the
Maze to another are partially Weave.
Hyperdimension: The hyperdimension class refers to the
dimension of
the object you move through the Maze, as opposed to the dimension of
the Maze
environment itself. Types are:
- Non-hypermaze:
Virtually all
Mazes, even those in higher dimensions or with special rules, are
normal non-hypermazes. In them you
work with a point or small object, such as a marble or yourself, which
you
move from point to point, where the path behind you forms a line.
There's an easily
countable number of choices
at each point.
- Hypermaze:
A hypermaze is where
the solving object is more than just a point. A standard hypermaze (or
a
hypermaze of the 1st order) consists of a line where as you bend and
move it
the path behind it forms a surface. A hypermaze can only exist in a 3D
or
higher dimension environment, where the entrance to a hypermaze is also
a line
instead of a point. A hypermaze is fundamentally different since you
need to
be aware of and work with multiple parts along the line at the same
time,
where there's nearly an infinite number of states and things you can do
with
the line at any time. The solving line is infinite, or the endpoints
are fixed
outside the hypermaze, to prevent one from crumpling the line into a
point, which could then be treated as
a non-hypermaze.
- Hyperhypermaze: Hypermazes can
be of arbitrarily high dimension. A hyperhypermaze (or a hypermaze of
the 2nd
order) increases the dimension of the solving object again. Here the
solving
object is a plane, where as you move it the path behind you forms a
solid. A
hyperhypermaze can only exist in a 4D or higher dimension environment.
Topology: The topology class describes the geometry of
the space the Maze exists in. Types are:
- Normal:
This
is a standard Maze in Euclidean space.
- Planair:
The term "planair"
refers to any Maze with an abnormal topology. This usually means
connecting the edges of the Maze in interesting fashions. Examples
are Mazes on the surface of a cube, Mazes on the surface of a
Moebius strip, and Mazes that are equivalent to being on a torus
with the left and right sides wrapping and the top and bottom
wrapping.
Tessellation: The tessellation class is the geometry of
the individual cells that compose the Maze. Types are:
- Orthogonal:
This is a standard rectangular grid where cells have passages
intersecting at right angles.
- Delta:
A Delta
Maze is one composed of interlocking triangles, where each cell
may have up to three passages connected to it.
- Sigma:
A Sigma
Maze is one composed of interlocking hexagons, where each cell
may have up to six passages connected to it.
- Theta:
Theta Mazes
are composed of concentric circles of passages, where the start
or finish is in the center, and the other on the outer edge.
Cells usually have four possible passage connections, but may
have more due to the greater number of cells in outer passage rings.
- Upsilon:
Upsilon
Mazes are composed of interlocking octagons and squares, where
each cell may have up to eight or four possible passages connected
to it.
- Zeta:
A Zeta Maze
is on a rectangular grid, except 45 degree angle diagonal passages
between cells are allowed in addition to horizontal and vertical
ones.
- Omega:
The term
"omega" refers to most any Maze with a consistent non-orthogonal
tessellation. Delta, Sigma, and Theta Mazes are all of this type,
as are many other arrangements one can think up, e.g. a Maze composed
of pairs of right triangles.
- Crack:
A crack
Maze is an amorphous Maze without any consistent tessellation,
but rather has walls or passages at random angles.
- Fractal:
A fractal Maze is a
Maze composed of smaller Mazes. A nested cell fractal Maze is a Maze
with other Mazes tessellated
within each cell, where the process may be repeated multiple times. An
infinite
recursive fractal Maze is a true fractal, where the Maze contains
copies of itself, and
is in effect an infinitely large Maze.
Routing: The routing class is probably the most interesting
with respect to Maze generation itself. It refers to the types
of passages within whatever geometry defined in the categories
above.
- Perfect:
A "perfect"
Maze means one without any loops or closed circuits, and without
any inaccessible areas. Also called a simply-connected Maze. From
each point, there is exactly one path to any other point. The
Maze has exactly one solution. In Computer Science terms, such
a Maze can be described as a minimal spanning tree over the set
of cells.
- Braid:
A "braid"
Maze means one without any dead ends. Also called a purely multiply
connected Maze. Such a Maze uses passages that coil around and
run back into each other (hence the term "braid") and
cause you to spend time going in circles instead of bumping into
dead ends. A well-designed braid Maze can be much harder than
a perfect Maze of the same size.
- Unicursal:
A
unicursal Maze means one without any junctions. Sometimes the
term Labyrinth is used to refer to constructs of this type, where
"Maze" means a puzzle where choices are involved. A
unicursal Maze has just one long snake-like passage that coils
throughout the extent of the Maze. It's not really difficult unless
you accidentally get turned around half way through and make your
way back to the beginning again.
- Sparseness:
A sparse Maze is one that doesn't have a passage through every cell,
where some are left uncreated. This amounts to having inaccessible
locations, making this somewhat the reverse of a braid Maze.
- Partial braid: A partial braid Maze is just a mixed
Maze with both loops and dead ends in it. The word "braid"
can be used quantitatively, where a "heavily braid Maze"
means one with many loops or detached walls, and a "slightly
braid Maze" means one with just a few.
Texture: The texture class is subtle, and describes the
style of the passages in whatever routing in whatever geometry.
They're not really on/off flags as much as general themes. Here
are several example variables one can look at:
- Bias:
A biased Maze
is one with straightaways that tend to go in one direction more
than the others. For example, a Maze with a high horizontal bias
will have long left-right passages, and only short up-down passages
connecting them. A Maze is usually more difficult to navigate
"against the grain".
- Run:
The "run"
factor of a Maze is how long straightaways tend to go before forced
turnings present themselves. A Maze with a low run won't have
straight passages for more than three or four cells, and will
look very random. A Maze with a high run will have long passages
going across a good percentage of the Maze, and will look similar
to a microchip.
- Elite:
The "elitism"
factor of a Maze indicates the length
of the solution with respect to the size of the Maze. An elitist
Maze generally has a short direct solution, while a non-elitist
Maze has the solution wander throughout a good portion
of the Maze's area. A well designed elitist Maze can be much harder
than a non-elitist one.
- Symmetric:
A symmetric Maze has symmetric passages, e.g. rotationally symmetric
about the
middle, or reflected across the horizontal or vertical axis. A Maze may
be
partially or totally symmetric, and may repeat a pattern any number of
times.
- River: The "river" characteristic means that
when creating the Maze, the algorithm will look for and clear
out nearby cells (or walls) to the current one being created,
i.e. it will flow (hence the term "river") into uncreated
portions of the Maze like water. A perfect Maze with less "river"
will tend to have many short dead ends, while a Maze with more
river will have fewer but longer dead ends.
Focus: The focus class is obscure, but shows that Maze
creation can be divided into two general types: Wall adders, and
passage carvers. This is more of an algorithmic difference when
generating, as opposed to a visual difference when observing,
but is still useful to consider. The same Maze can be often generated
in both ways:
- Wall adders: Algorithms that focus on walls start with
an empty area (or an outer boundary) and add walls. In real life,
a life size Maze composed of hedges, tarps, or wood walls, is
a definite wall adder.
- Passage carvers: Algorithms that focus on passages
start with a solid block and carve passages. In real life, a Maze
composed of mine tunnels, or running in the inside of pipes, is
a passage carver.
- Template:
Mazes can of course be both passage carved
and wall added, and some computer algorithms do just that. A Maze
template refers to a general graphic that isn't a Maze, which
is then modified to be a valid Maze in as few steps as possible,
but still has the texture of the original graphic template. Complicated
Maze styles like interlocking spirals are easier to do on a computer
as templates, as opposed to trying to create a valid Maze while
keeping it conforming to whatever style at the same time.
Other: The above is by no means a comprehensive list of
all possible classes or items within each class. They're just
the types of Mazes I've actually created. :-) Note
most every type of Maze, including Mazes with special rules, can be
expressed as
a directed graph, where you have a finite number of states and a finite
number
of choices at each state, which is called Maze
equivalence. Here are some other classes and types of Mazes:
- Direction:
This is where certain passages can only be traveled in one way.
In Computer
Science terms, such a Maze would be described by a directed graph,
as opposed to an undirected graph like all the others.
- Segmented:
This is where a Maze
has different sections of its area falling in different classes.
- Infinite
length Mazes: It's possible to create an infinitely long Maze
(a
finite number of columns by as many rows as you like) by only keeping
part of
the Maze in memory at a time and "scrolling" from one end to the
other, discarding earlier rows while creating later rows. One way is
with a
modified version of the Hunt and Kill algorithm. Visualize the
potentially
infinitely long Maze as a long film reel, composed of individual
picture
frames, where just two consecutive frames are kept in memory at a time.
Run
the Hunt and Kill algorithm, however give bias to the top frame so it
gets
finished first. Once finished, it's no longer needed, so can be printed
out,
etc. Either way, discard it, make the partially created bottom frame be
the
new top frame, and clear a new bottom frame. Repeat the process until
you
decide to stop, at which point let Hunt And Kill finish both frames.
The only
limitation is the Maze will never have a path that doubles back toward
the
entrance for a length greater than two frames. An easier way to make an
infinite Maze is with Eller's algorithm, as it already makes Mazes one
row at
time, so simply keep letting it add rows to the Maze forever.
- Virtual
fractal Mazes: A virtual
Maze is one where the whole Maze isn't stored in memory at once. For
example
only store the 100x100 section of passages or so nearest your location,
in a
simulation where you walk through a large Maze. An extension of nested
fractal Mazes
can be used to create virtual Mazes of enormous size, such as a billion
by a
billion passages. Note a life size version of a billion by billion Maze
(with
six feet between passages) would cover the Earth's surface over 19000
times!
Consider a 10^9 by 10^9 passage Maze, or a 10x10 Maze nested with 9
levels
total. If we want at least a 100x100 section around us, we only need to
create
the 100x100 passage submaze at the lowest level, and the seven 10x10
Mazes
it's nested within, to know exactly where the walls lie within a
100x100
section. (Actually it's best to have four adjacent 100x100 sections
forming a
square, in case you're near the edge or corner of a section, but the
same
concept applies.) To ensure the Maze remains consistent and never
changes as
you move around, have a formula to determine a random number seed for
each
coordinate at each nesting level. Virtual fractal Mazes are similar to
a
Mandelbrot set fractal, where the pictures in a Mandelbrot exist
virtually,
where you just need to visit a particular coordinate at a high enough
zoom
level for them to reveal themselves.
Here's a list of general algorithms to create the various classes of
Mazes
described above:
- Perfect:
Creating
a standard perfect Maze usually involves "growing" the Maze
while ensuring the no loops and no isolations restriction is kept.
Start with the outer wall, and add a wall segment touching it
at random. Keep on adding wall segments to the Maze at random,
but ensure that each new segment touches an existing wall at one
end, and has its other end in an unmade portion of the Maze. If
you ever added a wall segment where both ends were separate from
the rest of the Maze, that would create a detached wall with a
loop around it, and if you ever added a segment such that both
ends touch the Maze, that would create an inaccessible area. This
is the wall adding method; a nearly identical way to do it is
passage carved, where new passage sections are carved such that
exactly one end touches an existing passage.
- Braid:
To create
a Maze without dead ends, basically add wall segments throughout
the Maze at random, but ensure that each new segment added will
not cause a dead end to be made. I make them with four steps:
(1) Start with the outer wall, (2) Loop through the Maze and add
single wall segments touching each wall vertex to ensure there
are no open rooms or small "pole" walls in the Maze,
(3) Loop over all possible wall segments in random order, adding
a wall there if it wouldn't cause a dead end, (4) Either run the
isolation remover utility at the end to make a legal Maze that
has a solution, or be smarter in step three and make sure a wall
is only added if it also wouldn't cause an isolated section.
- Unicursal:
One
way to create a random unicursal Maze is to take a perfect Maze,
seal off the exit so there's only the one entrance, then add walls
bisecting each passage. This will turn each dead end into a U-turn
passageway, and there will be a unicursal passage starting and
ending at the original Maze's beginning, that will follow the
same path as someone wall following the original Maze. The new
unicursal Maze will have twice the dimensions of the original
perfect Maze it was based on. Small tricks may be done to have
the start and end not always be next to each other: When creating
the perfect Maze, never add segments attached to the right or
bottom walls, so the resulting Maze will have an easy solution
that follows that wall. Have the entrance at the upper right,
and after bisecting to create the unicursal routing, remove the
right and bottom wall. This will result in a unicursal Maze that
starts at the upper right and ends at the lower left.
- 3D:
Three and higher
dimensional Mazes can be created just like the standard 2D perfect
Maze, except from each cell you can move randomly to six instead
of four other orthogonal cells. These Mazes are generally passage
carved due to the extra dimensions.
- Weave:
Weave Mazes
are basically done as passage carved perfect Mazes, except when
carving a passage you're not always blocked by an existing passage,
as you have the option to go under it and still preserve the "perfect"
quality. On a monochrome bitmap, a Weave Maze can be represented
with four rows per passage (two rows per passage is enough for
a standard perfect Maze) where you have one row for the passage
itself and the other three rows to make it unambiguous when another
nearby passage goes under instead of just having a dead end near
the first passage. For aesthetics you may want to look ahead before
carving under an existing passage, to ensure you can continue
to carve once you're completely under it, so there won't be any
dead ends that terminate under a passage. Also, after carving
under a passage, you may want to invert the pixels adjacent to
the intersection, making it so newer passages can go over instead
of always under existing ones.
- Crack:
Crack Mazes
are basically done as wall added perfect Mazes, except there are
no distinct tessellation cells other than random pixel locations.
Pick a pixel that's already set as a wall, pick another random
location, and "shoot" or start drawing a wall toward
the second location. However, make sure you stop just before running
into any existing wall, so as not to create an isolation. Stop
after you haven't been able to add any significant walls in a
while. Note that random locations to draw to that may be anywhere
else in the Maze, will make it so there will be several straight
lines going across the Maze, and other proportionally smaller
walls as you look between them, the number of walls only being
limited by the pixel resolution. This makes the Maze look very
much like the surface of a leaf, so this is technically a fractal
Maze.
- Omega:
Omega style
Mazes involve defining some grid, defining how the cells link
up with each other, and how to map the vertexes that surround
each cell to the screen. For example, for the triangular Delta
Maze with interlocking triangular cells: (1) There's a grid where
each row has a number of cells that increases by two. (2) Each
cell is connected to the cells adjacent to it in that row, except
the third passage is linked to an appropriate cell in the row
above or below based on whether it's in an odd or even column
(i.e. whether the triangle is pointing up or down). (3) Each cell
uses the math for a triangle to figure out where to draw it on
the screen. You can draw all walls on the screen ahead of time
and passage carve the Maze, or keep some modified array in memory
and render the whole thing when complete.
- Hypermaze:
A hypermaze in a 3D
environment is similar to the reverse of a standard 3D non-hypermaze,
where
blocks become open spaces and vice versa. While a standard 3D Maze
consists of
a tree of passages through a solid area, a hypermaze consists of a tree
of
bars or vines through an open area. To create a hypermaze, start with
solid
top and bottom faces, then grow tangled vines from these faces to fill
the
space between, to make it harder to pass a line segment between the two
faces.
As long as each vine connects with either the top or bottom, the
hypermaze
will have at most a single solution. As long as no vine connects with
both the
top and bottom (which would form an impassable column), and as long as
there are
no vine loops in the top and bottom sections that cause them to be
inextricably
linked with each other like a chain, the hypermaze will be solvable.
- Planair:
Planair Mazes
with unusual topology are generally done as an array of one or
more smaller Mazes or Maze sections, where it's defined how the
edges connect with each other. A Maze on the surface of a cube
is just six square Maze sections, where when the part being created
runs into an edge it flows onto another section and onto the right
edge appropriately.
- Template:
Mazes based on templates are done by simply
starting with the base template image, then running the isolation
remover to ensure the Maze has a solution, followed by the loop
remover to ensure the Maze is hard enough, resulting in a perfect
Maze that still looks very similar to the original image. For
example, to create a Maze composed of interlocking spirals, just
create some random spirals without worrying whether it's a Maze
or not, then run it through the isolation and loop removers.
There are a number of ways of creating perfect Mazes, each with its
own characteristics. Here's a list of specific algorithms. All of these
describe creating the Maze by carving passages,
however unless otherwise specified each can also be done by adding
walls:
- Recursive
backtracker:
This is somewhat related to the recursive backtracker solving
method described below, and requires stack up to the size of the
Maze. When carving, be as greedy as possible, and always carve
into an unmade section if one is next to the current cell. Each
time you move to a new cell, push the former cell on the stack.
If there are no unmade cells next to the current position, pop
the stack to the previous position. The Maze is done when you
pop everything off the stack. This algorithm results in Mazes
with about as high a "river" factor as possible, with
fewer but longer dead ends, and usually a very long and twisty
solution. It runs quite fast, although Prim's algorithm is a bit
faster. Recursive backtracking doesn't work as a wall adder, because
doing so
tends to result in a solution path that follows the outside edge, where
the
entire interior of the Maze is attached to the boundary by a single
stem.
- Prim's
algorithm:
This requires storage proportional to the size of the Maze. During
creation, each cell is one of three types: (1) "In":
The cell is part of the Maze and has been carved into already,
(2) "Frontier": The cell is not part of the Maze and
has not been carved into yet, but is next to a cell that's already
"in", and (3) "Out": The cell is not part
of the Maze yet, and none of its neighbors are "in"
either. Start by picking a cell, making it "in", and
setting all its neighbors to "frontier". Proceed by
picking a "frontier" cell at random, and carving into
it from one of its neighbor cells that are "in". Change
that "frontier" cell to "in", and update any
of its neighbors that are "out" to "frontier".
The Maze is done when there are no more "frontier" cells
left (which means there are no more "out" cells left
either, so they're all "in"). This algorithm results
in Mazes with a very low "river" factor, with many
short dead ends, and the solution is usually pretty direct as
well. It also runs very fast when
implemented right, with only Eller's algorithm being faster.
- Kruskal's
algorithm:
This algorithm is interesting because it doesn't "grow"
the Maze like a tree, but rather carves passage segments all over
the Maze at random, but yet still results in a perfect Maze in
the end. It requires storage proportional to the size of the Maze,
along with the ability to enumerate each edge or wall between
cells in the Maze in random order (which usually means creating
a list of all edges and shuffling it randomly). Label each cell
with a unique id, then loop over all the edges in random order.
For each edge, if the cells on either side of it have different
id's, then erase the wall, and set all the cells on one side to
have the same id as those on the other. If the cells on either
side of the wall already have the same id, then there already
exists some path between those two cells, so the wall is left
alone so as to not create a loop. This algorithm yields Mazes
with a low "river" factor, but not as low as Prim's
algorithm. Merging the two sets on either side of the wall will
be a slow operation if each cell just has a number and are merged
by a loop. Merging as well as lookup can be done in near constant
time by giving each cell a node in a tree structure, with the
id at the root, where merging is done quickly by splicing the
trees together. Done right, this algorithm runs reasonably fast,
but not as fast as either of the above two, because of the edge
list and set management.
- Aldous-Broder
algorithm:
The interesting thing about this algorithm is it generates all possible
Mazes of a
given size with equal probability. It also requires no extra storage or
stack.
Pick a point, and move to a neighboring cell at random. If an uncarved
cell is
entered, carve into it from the previous cell. Keep moving to
neighboring
cells until all cells have been carved into. This algorithm yields
Mazes with
a low "river" factor, only slightly higher than Kruskal's algorithm.
(This means for a given size there are more Mazes with a low "river"
factor than high "river", since an average equal probability Maze
has low "river".) The bad thing about this algorithm is that it's
very slow, since it doesn't do any intelligent hunting for the last
cells,
where in fact it's not even guaranteed to terminate. However since the
algorithm is simple it can move over many cells quickly, so finishes
faster
than one might think. On average it takes about seven times longer to
run than
the above algorithms, although in bad cases it can take much longer if
the
random number generator keeps making it avoid the last few cells. This
can be
done as a wall adder if the boundary wall is treated as a single
vertex, i.e.
if a move goes to the boundary wall, teleport to a random point along
the
boundary before moving again. As a wall adder this runs nearly twice as
fast,
because the boundary wall teleportation allows quicker access to
distant parts
of the Maze.
- Wilson's
algorithm:
This is an improved version of the Aldous-Broder algorithm, in that it
produces
Mazes exactly like that algorithm, with all possible Mazes generated
with
equal probability, except that Wilson's algorithm runs much faster. It
requires storage up to the size of the Maze. Begin by making a random
starting
cell part of the Maze. Proceed by picking a random cell not already
part of
the Maze, and doing a random walk until a cell is found which is
already part
of the Maze. Once the already created part of the Maze is hit, go back
to the
random cell that was picked, and carve along the path that was taken,
adding
those cells to the Maze. More specifically, when retracing the path, at
each
cell carve along the direction that the random walk most recently took
when it
left that cell. That avoids adding loops along the retraced path,
resulting in
a single long passage being appended to the Maze. The Maze is done when
all
cells have been appended to the Maze. This has similar performance
issues as
Aldous-Broder, where it may take a long time for the first random path
to find
the starting cell, however once a few paths are in place, the rest of
the Maze
gets carved quickly. On average this runs five times faster than
Aldous-Broder,
and takes less than twice as long as the top algorithms. Note this runs
twice
as fast when implemented as a wall adder, because the whole boundary
wall
starts as part of the Maze, so the first walls are connected much
quicker.
- Hunt
and kill algorithm:
This algorithm is nice because it requires no extra storage
or stack, and is therefore suited to creating the largest Mazes
or Mazes on the most limited systems, since there are no issues
of running out of memory. Since there are no rules that must be
followed all the time, it's also the easiest to modify and to
get to create Mazes of different textures. It's most similar to
the recursive backtracker, except when there's no unmade cell
next to the current position, you enter "hunting" mode,
and systematically scan over the Maze until an unmade cell is
found next to an already carved into cell, at which point you
start carving again at that new location. The Maze is done when
all cells have been scanned over once in "hunt" mode.
This algorithm tends to make Mazes with a high "river"
factor, but not as high as the recursive backtracker. You can
make this generate Mazes with a lower river factor by choosing
to enter "hunt" mode more often. It runs slower due
to the time spent hunting for the last cells, but isn't much slower
than Kruskal's algorithm. This can be done as a wall adder if you
randomly
teleport on occasion, to avoid the issues the recursive backtracker
has.
- Growing
tree algorithm:
This is a general algorithm, capable of creating Mazes of different
textures. It requires storage up to the size of the Maze. Each
time you carve a cell, add that cell to a list. Proceed by picking
a cell from the list, and carving into an unmade cell next to
it. If there are no unmade cells next to the current cell, remove
the current cell from the list. The Maze is done when the list
becomes empty. The interesting part that allows many possible
textures is how you pick a cell from the list. For example, if
you always pick the most recent cell added to it, this algorithm
turns into the recursive backtracker. If you always pick cells
at random, this will behave similarly but not exactly to Prim's
algorithm. If you always pick the oldest cells added to the list,
this will create Mazes with about as low a "river" factor
as possible, even lower than Prim's algorithm. If you usually
pick the most recent cell, but occasionally pick a random cell,
the Maze will have a high "river" factor but a short
direct solution. If you randomly pick among the most recent cells,
the Maze will have a low "river" factor but a long windy
solution.
- Eller's
algorithm:
This algorithm is special because it's not only faster than all the
others that don't have obvious biases or blemishes,
but its creation is also the most memory efficient. It doesn't even
require
the whole Maze to be in memory, only using storage proportional to the
size of
a row. It creates the Maze one row at a time, where once a row has been
generated, the algorithm no longer looks at it. Each cell in a row is
contained in a set, where two cells are in the same set if there's a
path
between them through the part of the Maze that's been made so far. This
information allows passages to be carved in the current row without
creating
loops or isolations. This is actually quite similar to Kruskal's
algorithm,
just this completes one row at a time, while Kruskal's looks over the
whole
Maze. Creating a row consists of two parts: Randomly connecting
adjacent cells within a row, i.e. carving horizontal passages, then
randomly
connecting cells between the current row and the next row, i.e. carving
vertical passages. When carving horizontal passages, don't connect
cells
already in the same set (as that would create a loop), and when carving
vertical passages, you must connect a cell if it's a set of size one
(as
abandoning it would create an isolation). When carving horizontal
passages,
when connecting cells union the sets they're in (since there's now a
path
between them), and when carving vertical passages, when not connecting
a cell
put it in a set by itself (since it's now disconnected from the rest of
the
Maze). Creation starts with each cell in its own set before connecting
cells
within the first row, and creation ends after connecting cells within
the last
row, with a special final rule that every cell must be in the same set
by the
time we're done to prevent isolations. (The last row is done by
connecting
each pair of adjacent cells if not already in the same set.) One issue
with this algorithm is that
it's not balanced with respect to how it treats the different edges of
the
Maze, where connecting vs. not connecting cells need to be done in the
right
proportions to prevent texture blemishes.
- Recursive
division: This algorithm is somewhat similar to recursive
backtracking, since they're both stack based, except this focuses on
walls instead of passages. Start by making a random horizontal or
vertical wall crossing the available area in a random row or column,
with an opening randomly placed along it. Then recursively repeat the
process on the two subareas generated by the dividing wall. For best
results, give bias to choosing horizontal or vertical based on the
proportions of the area, e.g. an area twice as wide as it is high
should be divided by a vertical wall more often. This is the fastest
algorithm without directional biases, although it has the obvious
blemish of long walls crossing the interior. This algorithm is a form
of nested fractal Mazes, except instead of always making fixed cell
size Mazes with Mazes of the same size within each cell, it divides the
given area randomly into a random sized 1x2 or 2x1 Maze. Recursive
division doesn't work as a passage carver, because doing so results in
an obvious solution path that either follows the outside edge or else
directly crosses the interior.
- Binary
tree Mazes: This
is
basically the simplest and fastest algorithm possible, however Mazes
produced by it have a
very biased texture. For each cell carve a passage either leading up or
leading left, but not both. In the wall added version, for each vertex
add a wall segment leading down or right, but not both. Each cell is
independent of every other cell, where you don't have to refer to the
state of any other cells when creating
it. Hence this is a true memoryless Maze generation algorithm, with no
limit to the size of Maze you can create. This is basically a computer
science binary tree, if you consider the upper left corner the root,
where each node or cell has one unique parent which is the cell above
or to the left of it. Binary tree Mazes are different than
standard perfect Mazes, since about half the cell types can never exist
in them. For example there will
never be a crossroads, and all dead ends have passages pointing up or
left, and never down or right. The Maze tends to have passages leading
diagonally from upper left to lower right, where the Maze is much
easier to navigate from lower right to upper left. You will always be
able to travel up or left,
but never both, so you can always deterministically travel diagonally
up and to the left without hitting any barriers. Traveling down and to
the right is when you'll encounter choices and dead ends. Note if you
flip a binary tree Maze upside down and treat passages as walls and
vice versa, the result is basically another binary tree.
- Sidewinder
Mazes: This simple algorithm is very similar to the binary
tree algorithm, and only slightly more complicated. The Maze is
generated one row at a time: For each cell randomly decide whether to
carve a passage leading right. If a passage is not carved, then
consider the horizontal passage just completed, formed by the current
cell and any cells to the left that carved passages leading to it.
Randomly pick one cell along this passage, and carve a passage leading
up from it (which must be the current cell if the adjacent cell didn't
carve). While a binary tree Maze always goes up from the leftmost cell
of a horizontal passage, a sidewinder Maze goes up from a random cell.
While binary tree has the top and left edges of the Maze one long
passage, a sidewinder Maze has just the top edge one long passage. Like
binary tree, a sidewinder Maze can be solved deterministically without
error from bottom to top, because at each row, there will always be
exactly one passage leading up. A solution to a sidewinder Maze will
never double back on itself or visit a row more than once, although it
will "wind from side to side". The only cell type that can't exist in a
sidewinder Maze is a dead end with the passage facing down, because
that would contradict the fact that every passage going up leads back
to the start. A sidewinder Maze tends to have an elitist solution,
where the right path is very direct, but there are many long false
paths leading down from the top next to it.
| Algorithm |
Dead End % |
Type |
Focus |
Bias Free? |
Memory |
Time |
Solution % |
| Unicursal |
0 |
Tree |
Wall |
Yes |
N^2 |
261 |
100.0 |
| Recursive Backtracker |
10 |
Tree |
Passage |
Yes |
N^2 |
24 |
19.0 |
| Hunt and Kill |
11 (21) |
Tree |
Passage |
no |
0 |
55 (105) |
9.5 (3.9) |
| Recursive Division |
23 |
Tree |
Wall |
Yes |
N |
8 |
7.2 |
| Binary Tree |
25 |
Set |
Either |
no |
0* |
7 |
2.0 |
| Sidewinder |
27 |
Set |
Either |
no |
0* |
8 |
2.6 |
| Eller's Algorithm |
28 |
Set |
Either |
no |
N* |
10 |
4.2 (3.2) |
| Wilson's Algorithm |
29 |
Tree |
Either |
Yes |
N^2 |
51 (26) |
4.5 |
| Aldous-Broder Algorithm |
29 |
Tree |
Either |
Yes |
0 |
222 (160) |
4.5 |
| Kruskal's Algorithm |
30 |
Set |
Either |
Yes |
N^2 |
32 |
4.1 |
| Prim's Algorithm |
36 (31) |
Tree |
Either |
Yes |
N^2 |
21 |
2.3 |
| Growing Tree |
49 (39) |
Tree |
Either |
Yes |
N^2 |
43 |
11.0 |
This table summarizes the characteristics of the perfect Maze
creation
algorithms above. The Unicursal Maze algorithm (unicursal Mazes are
technically
perfect) is included for comparison. Descriptions of the columns follow:
- Dead End: This is the approximate percentage of cells
that are dead ends in a Maze created with this algorithm, when applied
to an orthogonal 2D Maze. The algorithms in the table are sorted by
this field. Usually creating by adding walls is the same as carving
passages, however if significantly different the wall adding percentage
is in parentheses. The Growing Tree value can actually range from 10%
(always pick newest cell) to 49% (always swap with oldest cell). With a
high enough run factor the Recursive Backtracker can get lower than 1%.
The highest possible dead end percentage in an 2D orthogonal perfect
Maze is 66%, which would be a unicursal passage with a bunch of one
unit long dead ends off either side of it.
- Type:
There are two types of perfect Maze creation algorithms: A tree based
algorithm grows the Maze like a tree, always adding onto what is
already present, having a valid perfect Maze at every step. A set based
algorithm builds where it pleases, keeping track of which parts of the
Maze are connected with each other, to ensure it's able to link
everything up to form a valid Maze by the time it's done.
- Focus: Most algorithms can be implemented by either
carving passages or adding walls. A few can only be done as one or the
other. Unicursal Mazes are always wall added since they involve
bisecting passages with walls, although the base Maze can be created
either way. Recursive Backtracker can't be done as a wall adder because
doing so tends to result in a solution path that follows the outside
edge, where the entire interior of the Maze is attached to the boundary
by a single stem. Similarly Recursive Division can only be done as a
wall adder due to its bisection behavior. Hunt and Kill is technically
only passage carved for a similar reason, although it can be wall added
if effort is made to grow inward from all boundary walls equally.
- Bias Free: This is whether the algorithm treats all
directions and sides of the Maze equally, where analysis of the Maze
afterward can't reveal any bias. Binary Tree is extremely biased, where
it's easy traveling toward one corner and hard to its opposite.
Sidewinder is also biased, where it's easy traveling toward one edge
and hard to its opposite. Eller's algorithm tends to have a passage
roughly paralleling the starting or finishing edges. Hunt and Kill is
nearly bias free, although the back and forth systematic searching will
give a slight bias along that axis.
- Memory: This is how much extra memory or stack is
required to implement the algorithm. Efficient algorithms only require
and look at the Maze bitmap itself, while others require storage
proportional to a single row (N), or proportional to the number of
cells (N^2). Some algorithms don't even need to have the entire Maze in
memory (these are marked with a asterisk). Eller's algorithm requires
storage for a row, but more than makes up for that since it only needs
to store the current row of the Maze in memory. Sidewinder also only
needs to store one row of the Maze, while Binary Tree only needs to
keep track of the current cell. Recursive Division requires stack up to
the size of a row, but other than that doesn't need to look at the Maze
bitmap any.
- Time: This gives an idea of how long it takes to create a
Maze using this algorithm, lower numbers being faster. The numbers are
only relative to each other (with the fastest standard algorithm being
assigned speed 10) as opposed to in some units, because the time is
dependent on the size of the Maze and speed of the computer. These
numbers are from creating 100x100 passage Mazes in the latest version
of Daedalus. Usually creating by adding walls is the same speed as
carving passages, however if significantly different the wall adding
time is in parentheses.
- Solution: This is the percentage of cells in the Maze
that the solution path passes through, for a typical Maze created by
the algorithm. This assumes the Maze is 100x100 passages with the start
and end in opposite corners. This is a measure of the "windiness" of
the solution path. Unicursal Mazes have maximum windiness, since the
solution goes throughout the entire Maze. Binary Tree has the minimum
possible windiness, where the solution path simply crosses the Maze and
never deviates away from or ceases to make progress toward the end.
Usually creating by adding walls has the same properties as carving
passages, however if significantly different the wall adding percentage
is in parentheses.
There are a number of ways of solving Mazes, each with its own
characteristics. Here's a list of specific
algorithms:
- Dead
end filler:
This is a simple Maze solving algorithm. It focuses on the Maze,
is always very fast, and uses no extra memory. Just scan the Maze,
and fill in each dead end, filling in the passage backwards from the
block until you reach
a junction. This includes filling in passages that become parts of dead
ends once other dead ends are removed. At the end only the solution
will remain, or solutions
if there are more than one. This will always find the one unique
solution for perfect Mazes, but won't do much in heavily braid
Mazes, and in fact won't do anything useful at all for those Mazes
without dead ends.
- Wall
follower:
This is another simple Maze solving algorithm. It focuses on you,
is always very fast, and uses no extra memory. Start following
passages, and whenever you reach a junction always turn right
(or left). Equivalent to a human solving a Maze by putting their
hand on the right (or left) wall and leaving it there as they
walk through. If you like you can mark what cells you've visited,
and what cells you've visited twice, where at the end you can retrace
the solution by following those cells visited once. This method won't
necessarily
find the shortest solution, and it doesn't work at all when the
goal is in the center of the Maze and there's a closed circuit
surrounding it, as you'll go around the center and eventually
find yourself back at the beginning. Wall following can be done in a
deterministic way in a 3D Maze by projecting the 3D passages onto the
2D plane, e.g. by pretending up passages actually lead northwest and
down lead southeast, and then applying normal wall following rules.
- Cul-de-sac
filler:
This method finds and fills in cul-de-sacs or nooses, i.e. constructs
in a Maze consisting of a blind alley stem that has a single loop
at the end. Like the dead end filler, it focuses on the Maze,
is always fast, and uses no extra memory. Scan the Maze, and for
each noose junction (a noose junction being one where two of the
passages leading from it connect with each other with no other
junctions along the way) add a wall to convert the entire noose
to a long dead end. Afterwards run the dead end filler. Mazes
can have nooses hanging off other constructs that will become
nooses once the first one is removed, so the whole process can
be repeated until nothing happens during a scan. This doesn't
do much in complicated heavily braid Mazes, but will be able to
invalidate more than just the dead end filler.
- Blind
alley filler:
This method finds all possible solutions, regardless of how long
or short they may be. It does so by filling in all blind alleys,
where a blind alley is a passage where if you walk down it in
one direction, you will have to backtrack through that passage
in the other direction in order to reach the goal. All dead ends
are blind alleys, and all nooses as described in the cul-de-sac
filler are as well, along with any sized section of passages connected
to the rest of the Maze by only a single stem. This algorithm
focuses on the Maze, uses no extra memory, but unfortunately is
rather slow. For each junction, send a wall following robot down
each passage from it, and see if the robot sent down a path comes
back from the same path (as opposed to returning from a different
direction, or it exiting the Maze). If it does, then that passage
and everything down it can't be on any solution path, so seal
that passage off and fill in everything behind it. This algorithm
will fill in everything the cul-de-sac filler will and then some,
however the collision solver will fill in everything this algorithm
will and then some.
- Blind
alley sealer: This is
like the blind alley filler, in that it also finds all possible
solutions by
removing blind alleys from the Maze. However this just fills in the
stem
passage of each blind alley, and doesn't touch any collection of
passages at
the end of it. As a result this will create inaccessible passage
sections for
cul-de-sacs or any blind alley more complicated than a dead end. This
algorithm
focuses on the Maze, runs much faster than the blind alley filler,
although it
requires extra memory. Assign each connected section of walls to a
unique set.
To do this, for each wall section not already in a set, flood across
the top
of the walls at that point, and assign all reachable walls to a new
set. After
all walls are in sets, then for each passage section, if the walls on
either
side of it are in the same set, then seal off that passage. Such a
passage
must be a blind alley, since the walls on either side of it link up
with each
other, forming a pen. Note a similar technique can be used to help
solve
hypermazes, by sealing off space between branches that connect with
each
other.
- Pledge
algorithm:
This is a modified version of wall following that's able to jump
between
islands, to solve Mazes wall following can't. It's a guaranteed way to
reach an
exit on the outer edge of any 2D Maze from any point in the middle,
however it's
not able to do the reverse, i.e. find a solution within the Maze. It's
great for
implementation by a Maze escaping robot, since it can get out of any
Maze without
having to mark or remember the path in any way. Start by
picking a direction, and always move in that direction when possible.
When a
wall is hit, start wall following until your chosen direction is
available
again. Note you should start wall following upon the far wall that's
hit, where
if the passage turns a corner there, it can cause you to turn around in
the
middle of a passage and go back the way you came. When wall following,
count the
number of turns you make, e.g. a left turn is -1 and a right turn is 1.
Only
stop wall following and take your chosen direction when the total
number of
turns you've made is 0, i.e. if you've turned around 360 degrees or
more, keep
wall following until you untwist yourself. The counting ensures you're
eventually able to reach the far side of the island you're currently
on, and
jump to the next island in your chosen direction, where you'll keep on
island
hopping in that direction until you hit the boundary wall, at which
point wall
following takes you to the exit. Note Pledge algorithm may make you
visit a
passage or the start more than once, although subsequent times will
always be
with different turn totals. Without marking your path, the only way to
know
whether the Maze is unsolvable is if your turn total keeps increasing,
although
the turn total can get to large numbers in solvable Mazes in a spiral
passage.
- Chain
algorithm: The Chain algorithm solves the Maze by
effectively treating it as a number of
smaller Mazes, like links in a chain, and solving them in sequence. You
have to specify the start and
desired end locations, and the algorithm will always find a path from
start to end if one
exists, where the solution tends to be a reasonably short if not the
shortest
solution. That means this can't solve Mazes where you don't know
exactly where
the end is. This is most similar to Pledge algorithm since it's also
essentially
a wall follower with a way to jump between islands. Start by drawing a
straight
line (or at least a line that doesn't double back on itself) from start
to end,
letting it cross walls if needed. Then just follow the line from start
to end.
If you bump into a wall, you can't go through it, so you have to go
around. Send
two wall following "robots" in both directions along the wall you hit.
If a robot
runs into the guiding line again, and at a point which is closer to the
exit,
then stop, and follow that wall yourself until you get there too. Keep
following
the line and repeating the process until the end is reached. If both
robots
return to their original locations and directions, then farther points
along the
line are inaccessible, and the Maze is unsolvable.
- Recursive
backtracker: This will find a solution, but
it won't necessarily find the shortest solution. It focuses on
you, is fast for all types of Mazes, and uses stack space up to
the size of the Maze. Very simple: If you're at a wall (or an
area you've already plotted), return failure, else if you're at
the finish, return success, else recursively try moving in the
four directions. Plot a line when you try a new direction, and
erase a line when you return failure, and a single solution will
be marked out when you hit success. When backtracking, it's best to
mark the
space with a special visited value, so you don't visit it again from a
different
direction. In Computer Science terms
this is basically a depth first search. This method will always
find a solution if one exists, but it won't necessarily be the
shortest solution.
- Tremaux's
algorithm: This Maze solving method is designed
to be able to be used by a human inside of the Maze. It's similar
to the recursive backtracker and will find a solution for all
Mazes: As you walk down a passage, draw a line behind you to mark
your path. When you hit a dead end turn around and go back the
way you came. When you encounter a junction you haven't visited
before, pick a new passage at random. If you're walking down a
new passage and encounter a junction you have visited before,
treat it like a dead end and go back the way you came. (That last
step is the key which prevents you from going around in circles
or missing passages in braid Mazes.) If walking down a passage
you have visited before (i.e. marked once) and you encounter a
junction, take any new passage if one is available, otherwise
take an old passage (i.e. one you've marked once). All passages
will either be empty, meaning you haven't visited it yet, marked
once, meaning you've gone down it exactly once, or marked twice,
meaning you've gone down it and were forced to backtrack in the
opposite direction. When you finally reach the solution, paths
marked exactly once will indicate a direct way back to the start.
If the Maze has no solution, you'll find yourself back at the
start with all passages marked twice.
- Collision solver: Also called the "amoeba"
solver, this method will find all shortest solutions. It focuses
on you multiple times, is fast for all types of Mazes, and requires
at least one copy of the Maze in memory in addition to using memory up
to the size of the Maze. It basically floods the Maze with
"water", such that all distances from the start are
filled in at the same time (a breadth first search in Computer
Science terms) and whenever two "columns of water" approach
a passage from both ends (indicating a loop) add a wall to the
original Maze where they collide. Once all parts of the Maze have
been "flooded", fill in all the new dead ends, which
can't be on the shortest path, and repeat the process until no
more collisions happen. (Picture amoebas surfing at the crest
of each "wave" as it flows down the passages, where
when waves collide, the amoebas head-butt and get knocked out,
and form there a new wall of unconscious amoebas, hence the name.)
- Shortest
path finder: As the name indicates, this algorithm
finds the shortest solution, picking one if there are multiple
shortest solutions. It focuses on you multiple times, is fast
for all types of Mazes, and requires quite a bit of extra memory
proportional to the size of the Maze. Like the collision solver,
this basically floods the Maze with "water", such that
all distances from the start are filled in at the same time (a
breadth first search in Computer Science terms) however each "drop"
or pixel remembers which pixel it was filled in by. Once the solution
is hit by a "drop", trace backwards from it to the beginning
and that's a shortest path. This algorithm works well given any
input, because unlike most of the others, this doesn't require
the Maze to have any one pixel wide passages that can be followed. Note
this is
basically the A* path finding algorithm without a heuristic so all
movement is
given equal weight.
- Shortest
paths finder:
This is very similar to the shortest path finder above, except
this finds all shortest solutions. Like the shortest path finder,
this focuses on you multiple times, is fast for all types of Mazes,
requires extra memory proportional to the size of the Maze, and
works well given any input since it doesn't require the Maze to
have any one pixel wide passages that can be followed. Also like
the shortest path finder, this does a breadth first search flooding
the Maze with "water" such that all distances from the
start are filled in at the same time, except here each pixel remembers
how far it is from the beginning. Once the end is reached, do
another breadth first search starting from the end, however only
allow pixels to be included which are one distance unit less than
the current pixel. The included pixels precisely mark all the
shortest solutions, as blind alleys and non-shortest paths will
jump in pixel distances or have them increase.
- Random mouse: For contrast, here's an inefficient Maze
solving method, which is basically to move randomly, i.e. move
in one direction and follow that passage through any turnings
until you reach the next junction. Don't do any 180 degree turns
unless you have to. This simulates a human randomly roaming the
Maze without any memory of where they've been. It's slow and isn't
guaranteed to ever terminate or solve the Maze, and once the end
is reached it will be just as hard to retrace your steps, but
it's definitely simple and doesn't require any extra memory to
implement.
| Algorithm |
Solutions |
Guarantee? |
Focus |
Human Doable? |
Passage Free? |
Memory Free? |
Fast? |
| Random Mouse |
1 |
no |
You |
Inside / Above |
no |
Yes |
no |
| Wall Follower |
1 |
no |
You |
Inside / Above |
Yes |
Yes |
Yes |
| Pledge Algorithm |
1 |
no |
You |
Inside / Above |
Yes |
Yes |
Yes |
| Chain Algorithm |
1 |
Yes |
You + |
no |
Yes |
no |
Yes |
| Recursive Backtracker |
1 |
Yes |
You |
no |
Yes |
no |
Yes |
| Tremaux's Algorithm |
1 |
Yes |
You |
Inside / Above |
no |
no |
Yes |
| Dead End Filler |
All + |
no |
Maze |
Above |
no |
Yes |
Yes |
| Cul-de-sac Filler |
All + |
no |
Maze |
Above |
no |
Yes |
Yes |
| Blind Alley Sealer |
All + |
Yes |
Maze |
no |
no |
no |
Yes |
| Blind Alley Filler |
All |
Yes |
Maze |
Above |
no |
Yes |
no |
| Collision Solver |
All Shortest |
Yes |
You + |
no |
no |
no |
Yes |
| Shortest Paths Finder |
All Shortest |
Yes |
You + |
no |
Yes |
no |
Yes |
| Shortest Path Finder |
1 Shortest |
Yes |
You + |
no |
Yes |
no |
Yes |
This table summarizes the characteristics of the Maze solving
algorithms above. Maze solving algorithms can be classified and judged
by these criteria. Descriptions of the columns follow:
- Solutions: This describes the solutions the algorithm
finds, and what the algorithm does when there's more
than one. An algorithm can pick one solution, or leave multiple
solutions. Also the solution(s) can be any path, or they can be the
shortest path. The dead end and cul-de-sac fillers (and the blind alley
sealer when considering its inaccessible sections) leave all solutions,
however they may also leave passages that aren't on any solution path,
so are marked "All +" above.
- Guarantee: This is whether the algorithm is guaranteed to
find at least one solution. Random mouse is "no" because it isn't
guaranteed to terminate, and wall follower and Pledge algorithm are
"no" because they will fail to find a solution if the goal is within an
island. The dead end and cul-de-sac fillers are "no" because they may
not do anything to the Maze at all in purely braid Mazes.
- Focus:
There are two general types of algorithms to solve a Maze: Focus
on "you", or focus on the Maze. In a you-focuser, you
have a single point ("You" above) or a set of points ("You +" above)
and try to move them through the Maze from
start to finish. In a Maze-focuser, you look at the Maze as a
whole and invalidate useless passages.
- Human Doable: This refers to whether a person could
readily use the algorithm to solve the Maze, either while inside
a life sized version, or while looking at a map from above. Some
you-focuser algorithms can be implemented by a person inside (or above)
the Maze, while some Maze-focusers can be implemented by a person, but
only from above. Other algorithms are complicated or intricate enough
they can only reliably be done by a computer.
- Passage Free: This is whether the algorithm can be done
anywhere. Some algorithms require the Maze to have obvious passages, or
distinct edges between distinct vertices in graph terms, or one pixel
wide passages when implemented on a computer. The wall follower, Pledge
algorithm, and chain algorithm only require a wall on one side of you.
The recursive backtracker and the shortest path(s) finders make their
own paths through open spaces.
- Memory Free: This is whether no extra memory or stack is
required to implement the algorithm. Efficient algorithms only require
and look at the Maze bitmap itself, and don't need to add markers to
the Maze during the solving process.
- Fast: This is whether the solving process is considered
fast. The most efficient algorithms only need to look at each cell in
the Maze once, or can skip sections altogether. Running time should be
proportional to the size of the Maze, or in Computer
Science terms O(n^2) where n is the number of cells along one
side. Random mouse is slow because it isn't guaranteed to terminate,
while the blind alley filler potentially solves the Maze from each
junction.
There are more things that can be done with Mazes beyond just creating
and
solving them, as described below:
- Flood
fill: A quick and dirty yet useful utility can
be implemented with a single call to a graphics library's Fill or
FloodFill routine. FloodFill the passage at the beginning, and
if the end isn't filled, the Maze has no solution. For Mazes with
an entrance and exit on the edges, FloodFill one wall, and the
remaining edge marks out the solution. For Mazes with the start
or goal inside the Maze, FloodFill the surrounding wall, and if
the exit wall isn't erased, wall following won't work to solve
it. Many Maze creation methods, solving methods, and other utilities
involve "flooding" the Maze at certain points.
- Isolation
remover: This means to edit the Maze such
that there are no passage sections that are inaccessible from
the rest of the Maze, by removing walls to connect such sections
to the rest of the Maze. Start with a copy of the Maze, then flood
the passage at the beginning. Scan the Maze (preferably in a random
order that still hits every possible cell) for any unfilled cells
adjacent to a filled cell. Remove a wall segment in the original
Maze at that point, flood the Maze at this new point, and repeat
until every section is filled. This utility is used in the creation
of braid and template Mazes.
- Loop
remover: This means to edit
the Maze such that there are no loops or detached walls within
it, every section of the Maze reachable from any other by at most
one path. The way to do this is almost identical to the isolation
remover, just treat walls as passages and vice versa. Start with
a copy of the Maze, then flood across the top of the outer walls.
Scan the Maze (preferably in a random other that still hits every
possible wall vertex) for any unfilled walls adjacent to a filled
wall. Add a wall segment to the original Maze at that point connecting
the two wall sections, flood the Maze at this new point, and repeat
until every section is filled. This utility is used in the creation
of template Mazes, and can be used to convert a braid Maze to
a perfect Maze that still looks similar to the original.
- Bottleneck
finder: This
means to find those passages or intersection points in a Maze such that
every solution to
that Maze passes through them. To do this, run the left hand wall
follower to
get the leftmost solution, and run the right hand wall follower to get
the
rightmost solution, where places the two solutions have in common are
the
bottlenecks. That technique however only works for Mazes that wall
following
will successfully solve. For other Mazes, to find bottleneck passages,
find any
solution to the Maze, and also run the
blind alley sealer (which may make the Maze unsolvable if it treats an
entrance or exit within the Maze as a large blind alley). Parts of the
solution
path that go through sealed off passages, are bottlenecks.
- Daedalus:
All the
Maze creation and solving algorithms described above are
implemented in Daedalus, a free Windows program available for download.
Daedalus comes with its complete source code, which can be viewed to
see more information about and specific implementations of these
algorithms.
This site produced by Walter
D. Pullen
(see Astrolog homepage),
hosted
on Magitech and astrolog.org,
created using Microsoft
FrontPage, page last updated March 3, 2009.
Top
Ten Maze Links:
- Mazes
for sale, ROYALTY FREE on Clip-Art website - http://www.clipartof.com
- Bearded
Bunny Blog - Free Printable Mazes - http://beardedbunnyblog.blogspot.com/2007/11/free-printable-mazes-from-4-great.html
- Team Of Monkeys - some
very cool mazes, for free and larger sizes and vectors files for sale
as clipart. - http://www.teamofmonkeys.com/
- Maze of Mazes - Collection
of image mazes. - http://mazeofmazes.net63.net
- Handy
Dandy Maze Editor - http://www.berighteous.com/euphoria/mazed.zip
- Experience
Mazes, REALLY! - http://www.abcfamilyadventures.co.uk/experience/mazes
- Maze
Master - Funky Mazes - http://www.mazemaster.com/MazeMaster/img/books/mm-ult002.jpg
- Ink Blot Mazes - Same
artist as Team Of Monkeys, but a much tidier site and also with
some quotes and other puzzles - http://www.inkblotmazes.com/
- Maze
Algorithms - Think Labyrinth - http://www.astrolog.org/labyrnth/algrithm.htm
- Mazes
on Facebook - an public album on facebook of mazes. COOL! - http://www.facebook.com/album.php?aid=16542&id=678580452&l=76507ed7ba
































